What Is Infinity?

    In Physics Ⅲ, Aristotle claims that magnitude is not infinite. So, no matter how much finite magnitude is added to a magnitude, the total magnitude is finite. That is, we cannot reach infinity by adding finite magnitude. This fact means that an arbitrary real number is finite. Firstly, an arbitrary natural number is finite. The proof by mathematical induction is below.

1. 1 is a finite number.
2. If n is a finite number, then n+1 is a finite number.
3. An arbitrary natural number is absolutely finite.

Secondly, an arbitrary integer is obviously finite. Thirdly, we can regard a rational number as a ratio of integers. Of course, an arbitrary rational number is finite. Finally, because a real number is a cut of rational numbers, an arbitrary real number is finite.

There Are Not Infinite Points on a Line Segment

    The Cantorians claim that there are infinite points on a line segment. However, in Area Is Essential for Euclidean Geometry, I described that we cannot detect a point on a line or an isolated point because a point has no extent. The reason why we cannot directly recognize a point is because only a surface reflects light, and then our eyes can recognize only light.
    Even so, we can detect a point as the end of a line. Our visual system extracts a line from the retinal bitmap image by the very complex data processing. In order to avoid complexity, figure 1 shows drastically simplified schema.

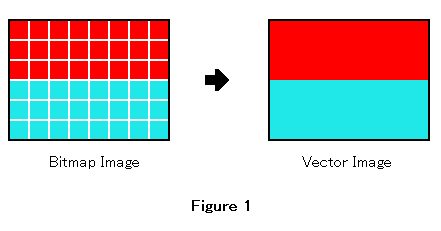
The left figure is the binary image, which consists of red and light blue pixels, and the right figure is the vector image, which consists of red and light blue areas. The bitmap image is converted into the vector image. In the vector image, we can see the line as the boundary between the red area and the light blue area. The line is the Euclidean line, which is the breadthless length. It is not the substantial entity. In order to clarify this fact more, figure 2 shows the eight division of the circle.

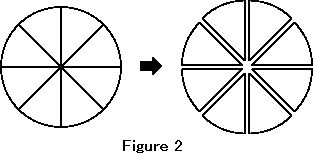
   The circle is divided into eight equal sectors. The left circle contains 9 points, but the right sectors contain 24 points. The division of the circle produces 15 points. However, the division does not change the total area and the total circumference. Only lines and points are divided. Especially, the central point is divided into 8 points. That is, a point can be divided without limit. Also, the circumference can be divided without limit. Therefore, there are not infinite points on a line segment, but the division of a line segment can produce points without limit.

What Is Potential Infinity?

    As mentioned above, there is not actual infinity. On the other hand, Aristotle proposes potential infinity.  In Physics Ⅲ, Aristotle described below: 

Now, as we have seen, magnitude is not actually infinite. But by division it is infinite. (There is no difficulty in refuting the theory of indivisible lines.) The alternative then remains that the infinite has a potential existence.

But the phrase 'potential existence' is ambiguous. When we speak of the potential existence of a statue we mean that there will be an actual statue. It is not so with the infinite. There will not be an actual infinite. The word 'is' has many senses, and we say that the infinite 'is' in the sense in which we say 'it is day' or 'it is the games', because one thing after another is always coming into existence. For of these things too the distinction between potential and actual existence holds. We say that there are Olympic games, both in the sense that they may occur and that they are actually occurring.

The infinite exhibits itself in different ways-in time, in the generations of man, and in the division of magnitudes. For generally the infinite has this mode of existence: one thing is always being taken after another, and each thing that is taken is always finite, but always different. Again, 'being' has more than one sense, so that we must not regard the infinite as a 'this', such as a man or a horse, but must suppose it to exist in the sense in which we speak of the day or the games as existing things whose being has not come to them like that of a substance, but consists in a process of coming to be or passing away; definite if you like at each stage, yet always different.

Potential infinity is realized as the infinite loop on the digital computer. For example, below is the algorithm to print 1 repeatedly without limit.

1. Print 1
2. Return to step 1

Using above algorithm, we can print 1 without limit, but the number of printed 1 is finite at any time. Because the passed time is finite at any given time, it is impossible that infinite time has passed. Therefore, potential infinity is finite without limit. 

Table of Contents